2. MLP入门
MLP 入门
1. MLP 算法简单推导
识别手写数字为例:假设样本为 n 个手写数字图像,每个数字图像由 28×28 像素组成,每个像素由灰度值表示。
我们把 28×28 的像素展开变成一个有 784 个维度的一维行向量,即一个样本向量,那么此时 =>
输入层:每个神经元对应一个像素点,共 784 个神经元
因为是识别单个手写数字,其结果会有 0-9 这十种情况,因此 =>
输出层:10 个神经元
隐藏层:层数以及单元数则作为要优化的额外超参数,设为 q
p.s. 关于激活函数:
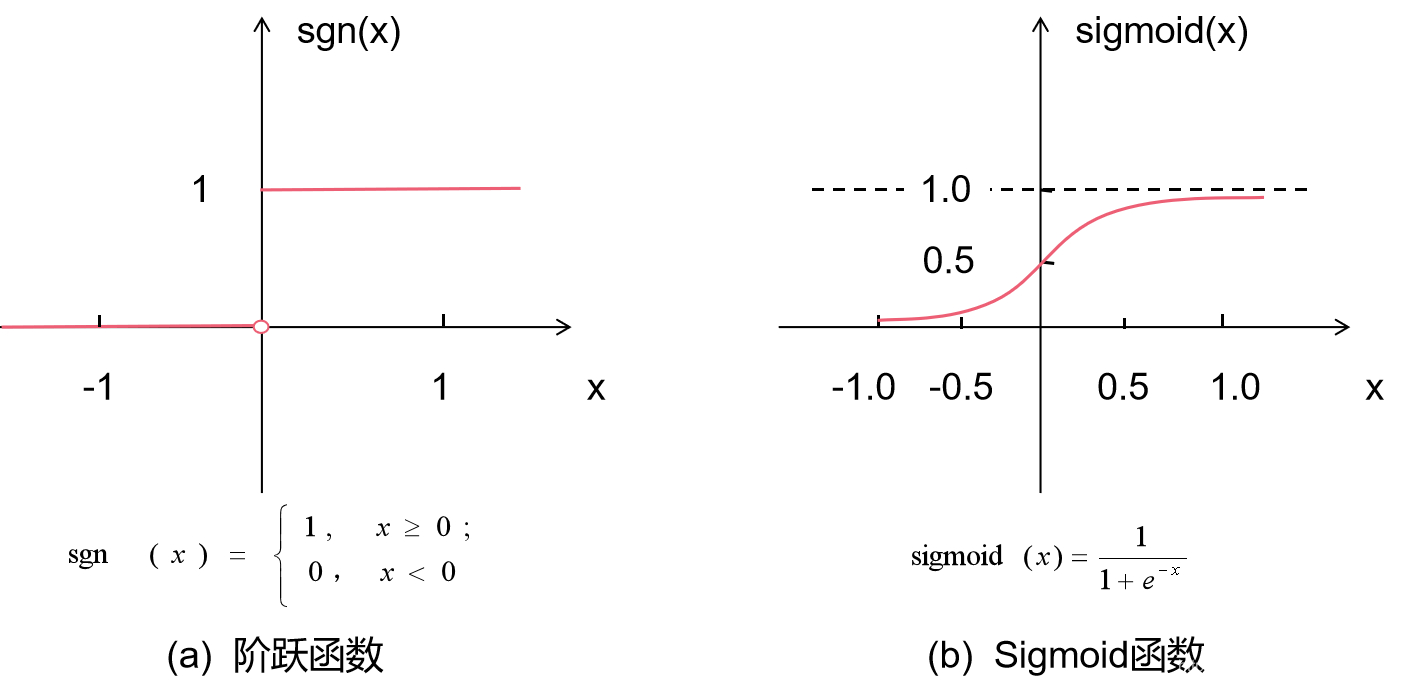
理想的激活函数是如下图(a)所示的阶跃函数,它将输入值映射为输出值“0”或“1”,显然“1”对应于神经元兴奋,“0”对应于神经元抑制;
然而,阶跃函数具有不连续、不光滑等不太好的性质,因此实际常用 Sigmoid 函数作为激活函数,如下图(b)所示。
【有时,输出层神经元也采用线性激活函数,即直接以输入值 c 与阈值 θ 的比较结果作为最后的预测值 y’输出。】
2. 正向传播(Forward Propagation):激活神经网络
n 个样本向量组成的矩阵 X 的维度为 n×784,每一行为一个样本向量;这也我们得到输入矩阵:
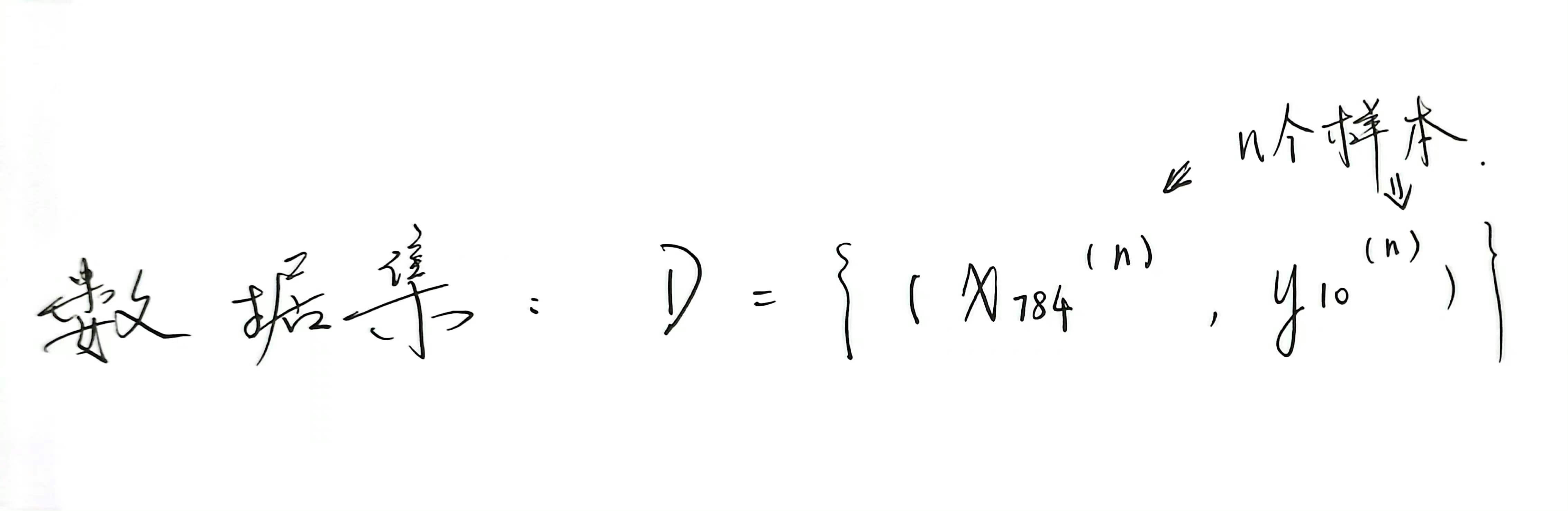
而后,隐藏层输入数据:

接下来,隐藏层的各个功能神经元将接收到的输入值 ah(h=1,2,…,q),与某一阈值 γh(h=1,2,…,q)进行比较,
然后通过激活函数 Sigmoid 处理产生神经元的输出 bh(h=1,2,…,q),用公式表示为:
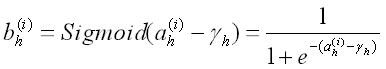
于是,隐藏层输出向量为:
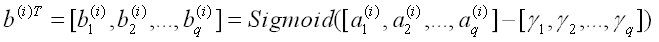
之后,隐藏层神经元的输出 bh(h=1,2,…,q)继续通过带权重的连接 w 传递至输出层,成为输出层的输入值 co(o=1,2,…,l),
同理,参照上面的 V 矩阵可知此处的 W 的转置 将是一个 q×l 的矩阵;
同理 Sigmoid 处理:
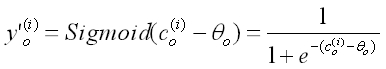
后得到:
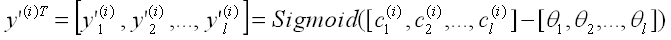
3. 逆向传播(Back Propagation):学习权重系数及阈值
大致流程思路:
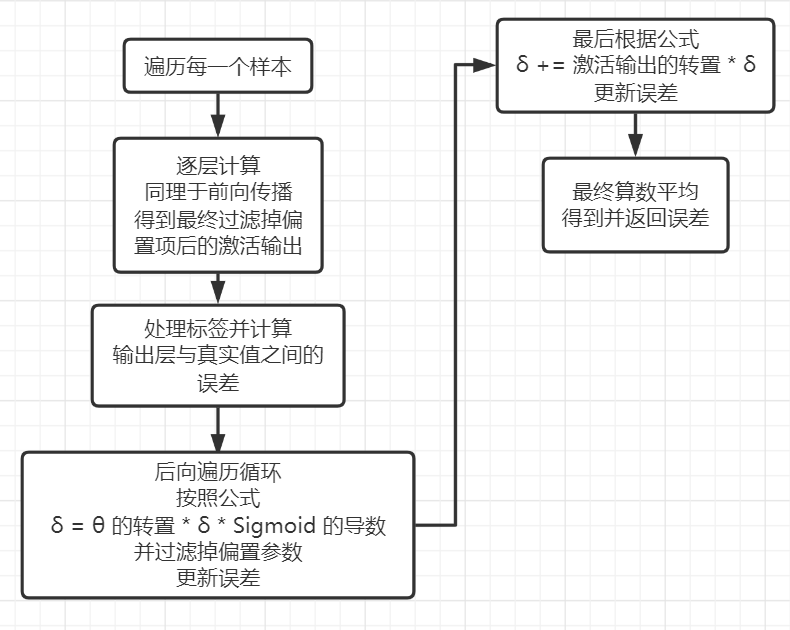
学习一个最基本却应用十分广泛的方法:梯度下降法(Gradient Descent);
梯度下降可以说是神经网络最常用的优化算法,其原理:
目标函数 J(θ)关于参数 θ 的梯度将是损失函数(loss function)上升最快的方向。
而我们要最小化 loss,只需要将参数沿着梯度相反的方向前进一个步长,就可以实现目标函数的下降。
这个步长 η 又称为学习速率。
更新参数的公式为: θ = θ - η * ∇J(θ)
损失函数上升的方向是坏的,把他当成比较累的上山;
也就是说梯度就是上山;
所以我们要最小化损失函数,也就是要往下山的方向前进步长;
那么下山的速度也就是步长、学习速率 η。
于是我们发现了步长 η 还是蛮重要的:
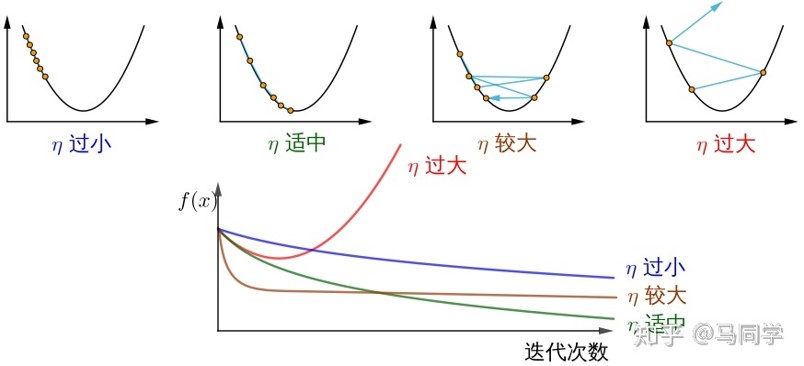
回到数学上来,如下图所示:
 这种大幅的上下波动,减慢了梯度下降法的速度;
这种大幅的上下波动,减慢了梯度下降法的速度;
且前文已知无法使用更大的学习率,因为如果用较大的学习率,可能降低效率甚至偏离函数的范围。
虽然近处的步 η 长大,但因算术平均导致权重较小,这样对梯度下降速度影响的贡献不够大。
这就要引入一个优化梯度下降算法的基本方法:
指数加权平均:
比如 t 时刻的观测值为 x(t) ,那么评估 t 时刻的移动平均值为:
v(t) = η * x(t) + (1 - η) * v(t-1) η 取 0~1
递推展开后可知,x 的权重是在指数递减的
也就是说,最近的观测值对 v 的影响最大,也即横轴上将学习得更快
进一步的,为了减少这些摆动,使得近处在纵轴上的学习减速,同理加权平均
于是我们就有了 动量法(Momentum),
它在每次计算梯度的迭代中,对 dw 和 db 使用了指数加权平均法的思想:

并最终得到更高效的算法:
